BINARY SEARCH TREE (BST)

Binary Search Tree (BST) merupakan sebuah konsep untuk penyimpanan data , yang dimana data yang disimpan dalam bentuk tree(pohon) yang setiap node yang memiliki anak maksimal 2 anak / 2 node. Kegunaan dari Binary Search Tree (BST) juga untuk melakukan pencarian dan melakukan sorting secara lebih efisien.

Ciri-citi dari Binary Search Tree (BST) adalah:
1.Value dari node kiri lebih kecil dibandingkan rootnya.
2.Value dari node kanan lebih besar dibandingkan dengan rootnya.
3.Setiap node harus memiliki value dan tidak ada valuenya yang berisikan double/float.

Fungsi-fungsi yang terdapat di dalam Binary Search Tree (BST):
1.Find(x) = Berfungsi untuk melakukan pencarian value (x) pada BST.
2.Insert(x) = Berfungsi untuk memasukkan value (x) yang baru ke dalam BST.
3.Remove(x) = Berfungsi untuk menghapus value (x) yang ada di dalam BST.

Fungsi Find(x) / Mencari Data
-) Memulai pencarian dari root.
-) Jika root adalah value yang kita cari , maka program selesai.
-) Jika x lebih besar dari root maka akan mencari secara rekursif ke tree sebelah kanan.
-) Jika x lebih kecil dari root maka akan mencari secara rekursif ke tree sebelah kiri.

Fungsi Insert(x) / Memasukkan Data
-)Dimulai dari root pertama.
-) Jika x lebih kecil dari node value kemudian mengecek dengan subtree sebelah kiri lakukan pengecekan secara rekursif.
-) jika x lebih besar dari node value kemudian mengecek dengan subtree sebelah kanan lakukan pengecekan secara rekursif.
-) Lakukan secara terus menerus hingga mendapatkan node yang kosong lalu diisi.

Fungsi Remove(x) / Menghapus Data
-) Jika value yang ingin dihapus merupakan leaf(daun) atau paling bawah. maka value akan langsung di remove.
-) Jika value yang ingin dihapus mempunyai 1 anak, maka hapus nodenya dan gabungkan anaknya ke parent yang belum dihapus.
-)Jika value yang akan dihapus mempunyai 2 anak, maka ada 2 cara yaitu:
   1.Node akan digantikan oleh node paling kiri dari subtree kanan.
   2.Node dapat digantikan oleh node paling kanan dari subtree kiri.

Hashing Table dan Binary tree

HASHING TABLE & BINARY TREE

Hashing
Hashing adalah transformasi aritmatik sebuah string dari karakter menjadi nilai yang merepresentasikan string aslinya. Hasing digunakan sebagai metode untuk menyimpan data dalam sebuah array agar penyimpanan data, pencarian data, penambahan data dan penghapusan data dapat dilakukan dengan lebih cepat.

Hash Table
Hash Table adalah sebuah struktur data yang terdiri atas sebuah table dan fungsi yang bertujuan untuk memetakan nilai kunci yang unik untuk setiap recor(baris) menjadi angka(hash) lokasi record tersebut dalam sebuah table.

Operasi yang terdapat pada Hash Table

1. Insert : diberikan sebuah key dan nilai, insert nilai dalam table.
2. Find : diberikan sebuah key, temukan nilai yang berhubungan dengan key.
3. Remove : diberikan sebuah key, temukan nilai yang berhubungan denganan key kemudian hapus nilai tersebut.
4. getIterator : mengembalikan iterator, yang memeriksa nilai satu demi satu.

Implementasi hashing table in blockchain

Hashing table memiliki peranan dalam menajga keamanan data atau disebut crypthographic dan hubungannya dengan blockchain adalah blockhain merupakan catatan traksaksi digital yang dihubungkan dari individu dan dihubungkan ke daftar. Sehingga blockchain sangat memerlukan hashing table untuk menjaga keamanan datanya.

Salah satu contoh teknologi yang menggunakan blockchain adalah bitcoin. Fungsi dari hash di dalam bitcoin adalah untuk menambahkan data baru ke dalam blockchain dengan cara menambang. Sehingga hash berperan penting agar data yang sedang diproses menjadi lebih aman karena prosesnya yang lama.

TREE
Tree merupakan salah satu bentuk struktur data tidak linear yang menggambarkan hubungan yang bersifat hirarkir(hubungan one to many) antar elemen. Tree juga bisa disimpulkan sebagai kumpulan simpul/node dengan satu elemen khusus yang disebut root dan node lainnya terbagi menjadi himpunan-himpunan yang saling tak berhubung satu sama lain(subtree).


Binary Tree:
Binary Tree merupakan tree yang memiliki hanya 2 child disetiap nodenya dan tidak boleh kurang.

Jenis-jenis Binary Tree:

• Full Binary Tree : Binary tree yang tiap nodenya (kecuali leaf) memiliki dua child dan setiap subtree harus mempunyai panjang path yang sama.
• Complete Binary Tree : Tiap subtree boleh memiliki panjang path yang berbeda tapi node kecuali leaf memiliki 0 atau 2 child.

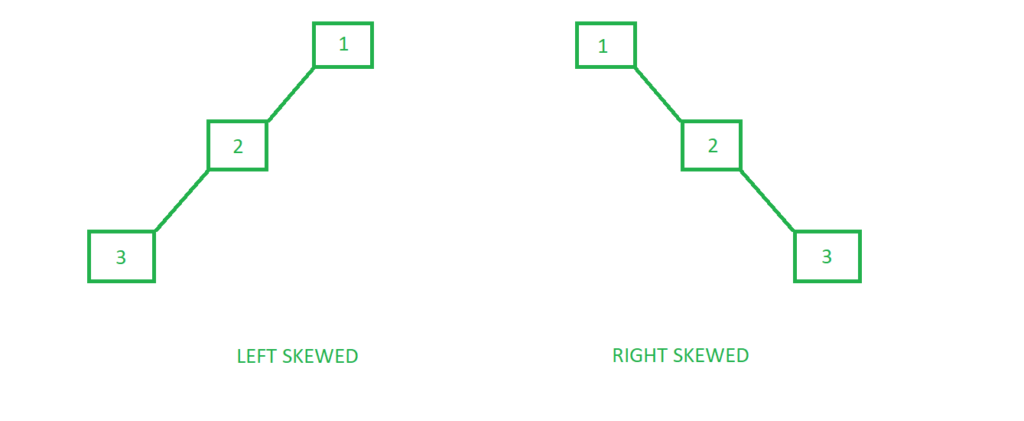
• Skewed Binary Tree : Binary Tree yang semua nodenya (kecuali leaf) hanya memiliki 1 child.

Stack dan Queue

STACK

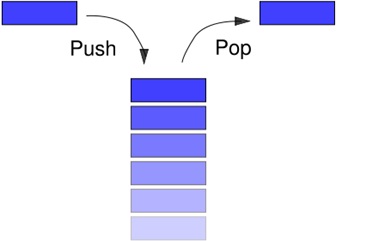
Stack merupakan salah satu struktur data yang sistem kerjanya LIFO (Last In First Out) yang dimana bermaksud data yang terakhir masuk juga merupakan data yang pertama kali keluar. Data hanya dapat diakses melalui satu titik saja yaitu atas atau biasa disebut sebagai TOP. Stack sendiri dapat diilustrasikan seperti saat kita akan mencuci piring , tumpukan piring teratas yang akan kita cuci terlebih dahulu.

Fungsi-fungsi yang terdapat di dalam stack:

1. Push : digunakan untuk menambah item pada stack pada tumpukan paling atas.
2. Pop : digunakan untuk mengambil item pada stack pada tumpukan paling atas.
3. Clear : digunakan untuk mengosongkan stack.
4. Create stack : digunakan untuk membuat tumpukan S baru, dengan jumlah elemen kosong.
5. MakeNull : mengosongkan Tumpukan S, jika ada elemen maka semua elemen dihapus.
6.  IsEmpty : fungsi yang digunakan untuk mengecek apakah Stack sudah kosong.
7. Isfull : fungsi yang digunakan untuk mengecek apakah Stack sudah penuh.

QUEUE

Queue adalah kumpulan data yang dimana penambahan datanya hanya dapat melalu satu sisi, yaitu dari belakang atau juga biasa disebut sebagai TAIL dan pengahapusan data hanya dapat dilakukan dari sisi sebaliknya yaitu depan atau bisa disebut sebagai HEAD. Sistem kerja pada Queue adalah FIFO(First In First Out) yang bermaksud data yang pertama kali dimasukkan akan menjadi data pertama juga yang keluar.

Fungsi-fungsi yang terdapat pada Queue:

1. Create() : berfungsi untuk menciptakan dan menginisialisasikan Queue.
2. IsEmpty() : berfungsi untuk memeriksa apakah antrian kosong.
3. IsFull() : berfungsi untuk mengecek apakah antrian sudah penuh.
4. Enqueue() : berfungsi untuk menambahkan elemen (penambahan elemen selalu ditambahkan di elemen paling belakang)
5. Dequeue() : berfungsi untuk menghapus elemen terdepean atau HEAD dari antrian.
6. Clear() : berfungsi untuk menghapus elemen-elemen antrian dengan cara membuat TAIL dan HEAD = -1.
7. Tampil() : Untuk menampilkan nilai-nilai elemen antrian.

INFIX , POSTFIX, PREFIX

Infix adalah notasi yang terbentuk berdasarkan operator yang berada di antara operand seperti pada contoh diatas A + B , A dan B merupakan operand dan ditengahnya ada operator yaitu '+', biasanya infix digunakan untuk melakukan perhitungan aritmatika.

Postfix adalah cara penulisan notasi yang menuliskan operand terlebih dahulu baru operator dibelakangnya seperti contoh diatas A dan B merupakan operand dan pada akhirnya diikuti oleh '+' sebagai operator.

Prefix adalah cara penulisan notasi dengan meletakkan operator di depan operand tanpa adanya tanda kurung. Seperti contoh diatas operator berada didepan dan operand mengikuti dibelakang operator.